几何问题的考察侧重于个人的空间能力,而很多的人对于空间能力的运用并不是很到位,因此在做几何问题时很吃力。几何问题的基础是熟记相关公式及性质,而三角形又是几何问题中一个重要考点,所以必须掌握。接下来带各位考生一起来学习几何问题。
一、公式及性质
三角形涉及的公式不多,其中面积较为容易求解,面积=(底×高)÷2,而三边均可为底,应理解为:三边与之对应的高的积的一半是三角形的面积。对于直角三角形,还需要记住勾股定理的公式。
三角形的基本性质是三边关系:三角形任意两边之和大于第三边,任意两边之差小于第三边。
【例1】有两根长度分别为4cm,9cm的木棒,若想钉一个三角形木架,现有五根长度分别为3cm,6cm,11cm,12cm,13cm木棒供选择,可选择的方法有几种( )
A.1 B.2 C.3 D.4
5,而<13.则其中的6,11,12符合。故选C。
考试中常考的性质是三角形的相似:相似三角形对应边成比例,对应角相等。但是不同于高考,行测考试不会考察证明,重在应用。
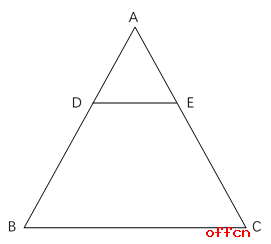
【例2】已知,DE∥BC,E为AC的三等分点,DE长度为5cm,求BC长度为多少?
A.10 B.15 C.20 D.25
【答案】B。解析:三角形ADE与三角形ABC相似,E为三等分点,则AE/AC=1/3,则相似比为1/3,所以DE/BC=1/3,BC=3DE=15。答案选B。
经过题目分析会发现几何题目重在发现几何规律,然后根据相关性质进行求解。三角形相似作为基础知识,还请广大考生一定要熟练。
二、经典例题
【例1】一直角三角形,其最长的边为15cm,最短的边为9cm,则该三角形的面积比周长的数值大多少( )?
A.18 B.54 C.36 D.27
【答案】A。解析:首先,此三角形为直角三角形,其最长的边为15,最短的边为9说明其斜边长为15,一个直角边为9,运用勾股定理可知,另一直角边的长度为12。该三角形的面积为(12×9)/2=54;该三角形的周长为:15+12+9=36;54-36=18,所以该题目选A.。
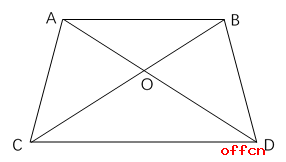
【例2】如图,梯形ABCD的两条对角线AD、BC相较于O点,已知三角形ABO的面积是1,且AB:CD=1:2, 求梯形ABCD的面积是多少?
A.4 B.7 C.9 D.11
【答案】C。解析:由图可得三角形ABO和COD相似,相似比为1:2,则面积比为1:4,即三角形COD面积为4,又因为AO与DO之比为1:2,所以三角形AOC与三角形DOC面积比为1:2,则三角形AOC面积为2,同理可得三角形BOD面积为2,则梯形面积为1+4+2+2=9。选C。








