容斥是研究集合与集合之间交叉关系的一类题型，题目的难度并不是很大，若能够掌握它的本质，熟练运用解题方法便可以快速求解，找到答案;值得广大考生注意的一点是容斥问题现在不只是单一公式的考察，更多的是结合排列组合、概率等题目进行测查，需要做到掌握本质，学习绘制文氏图。
一、 容斥问题基本公式
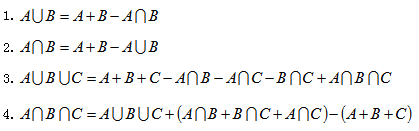
二、容斥的极值问题
设集合为A,B,C,D;全集为U
1.两个集合A、B交集的最小值为A+B-U
三个集合A、B、C交集的最小值为A+B+C-2U
四个集合A、B、C、D交集的最小值为A+B+C+D-3U
2.N个集合交集的最大值均为较小的集合
三、例题
1.某公司招聘员工，按规定每人至多可投考两个职位，结果共42人报名，甲、乙、丙三个职位报名人数分别是22人、16人、25人，其中同时报甲、乙职位的人数为8人，同时报甲、丙职位的人数为6人，那么同时报乙、丙职位的人数为：
A.7人 B.8人 C.5人 D.6人
【答案】A。解析：根据题意，“按规定每人至多可投考两个职位”则表明这次招聘中不存在有人报考三个职位的情形，共有42人报名，也表明不存在一个人是三个职位都不报考的情形。故可以直接代入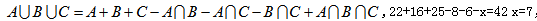
，故选择A选项。
2.某企业从10名高级管理人员中选出3人参加国际会议。在10名高级管理人员中，有一线生产经验的有6人，有研发经验的有5人，另有2人既无一线生产经验也无研发经验，如果要求选出的人中具备一线生产经验的人和具备研发经验的人都必须有。问有多少种不同的选择方式?
A.96 B.100 C.106 D.112
【答案】C。解析：有一线生产经验或者研发经验的共有8人，则只有一线生产经验的有8-5=3人，只有研发经验的有8-6=2人，既有一线生产经验，又有研发生产经验的也有3人，2个人全无，根据间接法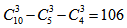
，选择C。
所以这部分题目是大家在考试时可以选择的。并且大部分的题目，背景越来越贴近生活实际，但同时我们在做题的时候也不能固化思维还是要学会活学活用。
