在每年的各类考试中，极值问题都是常考的一类题目，极值问题其实是非常简单的一类题目，只要掌握基本公式和结论。就能快速解题，下面小编就来带大家了解极值问题当中的一类问题—均值不等式。
什么是均值不等式
定理1：若a、b是实数，则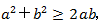
，等号当且仅当a=b时取得。
推论1：若a、b是正实数，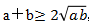
，等号当且仅当a=b时取得。
定理2：若a、b、c是正实数，则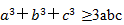
，等号当且仅当a=b=c时取得。
推论2：若a、b、c是正实数，则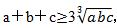
，等号当且仅当a=b=c时取得。
均值不等式的应用
(1) 和一定，求积的最大值。
例1：3个自然数之和为14，它们的乘积的最大值是多少?
A.42 B.84 C.100 D.120
【答案】C。解析：三个数的和一定，要想使积最大，则需要使这几个数尽量接近，取5、5、4，所以积最大为100。C选项正确。
(2) 积一定，求和的最小值。
例2：若两个自然数的积为100，则这两个自然数和的最小值为多少?
A.10 B.20 C.30 D.40
【答案】B。根据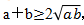
，可得这两个自然数的和
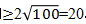。所以，这两个自然数和的最小值为20。B选项正确。
例3：用18米长的警戒线围成各种长方形，要求长和宽的长度都是整数米。围成的长方形面积最大是多少?
A.18平方米 B.20平方米 C.25平方米 D.40平方米
【答案】B。长方形的周长为18米，长方形面积为长×宽，则长+宽为定值9，两个数和为定值，要想使两个数积最大，则需使两个数尽量接近，又因长和宽都是整数米，则长和宽分别为4和5，面积最大为4×5=20。B选项正确。
通过上面几道题的练习，相信大家已经熟悉并掌握了均值不等式，同时大家也会发现数量关系在考试过程中其实并不难，更多的都是贴近我们日常生活的问题，所以大家要认真学习数量关系的奥秘。
