概率问题是行测考试中常见的题型，因为概率求解的是事情发生的可能性大小，一般的等可能事件都有一个公式来进行求解，那就是
，也就是说想要求概率就要知道这两个等可能事件样本数，而事件的样本数我们怎么求解呢，一种就是一个一个的枚举出来，而当样本比较多的时候一一的去枚举势必浪费时间。那就可以借助排列组合作为一个工具来帮助我们计算，这就意味着，排列组合中比较重要的分类分步思想是可以同样适用的，今天就带大家来看一下分类分步是怎么应用到实际的概率解题中。
例1：一位乒乓球学员手中拿着装有7只乒乓球的不透明口袋，其中有3只黄球，4 只白球。他随机取出一只乒乓球，观察颜色后放回袋中，同时放人2只与取出的球同色的球。这样连续取2次，则他取出的两只球中第1次取出的是白球，第2次取出的是黄球的概率是：
【解析】根据题意，第一次取出白球的概率为 然后将两只白球放入袋中，此时袋中有9只球，第二次取出黄球的概率为
，所求概率为
。故本题选B。
例2：某仓库存放三个厂生产的同一品牌洗衣液，其中甲厂生产的占20%，乙厂生产的占30%，剩余为丙厂生产的，且三个厂家的次品率分别为1%、2%、 1%. 则从仓库中随机取出一件是次品的概率为:
A.1% B.1.3% C.1.6% D.2%
【解析】根据题意，该次品可以出自甲、乙、丙，则从仓库中取出一件次品的概率为20%×1%+20%×2%+50%×1%=1.3%.故本题选B。
题目中出现多台机器或者多个人去做某项工程，设每台机器或者每个人单位时间的效率为1。
例3：在十字路口处，一辆汽车的行驶方向有3个：直行、左转弯、右转弯，且三种可能性大小相同，则有3辆车独立行驶的汽车经过该十字路口全部右转弯的概率是：
【解析】根据题意，每辆车右转弯的概率都是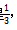
三辆独立行驶的车都右转弯的概率为
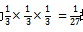故本题选D。
总结：遇见多种事件放到一起求解的概率就可以用分类分步的思路来解决，希望能帮助大家解题。
