龟兔赛跑的故事源于伊索寓言，可谓众所周知，按照龟兔赛跑的故事情节，兔子和乌龟的位移图象如图所示，下列关于兔子和乌龟的运动正确的是A．兔子和乌龟是同时从同_高中物理题库

题文

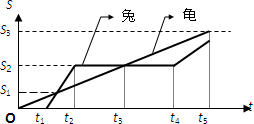
龟兔赛跑的故事源于伊索寓言，可谓众所周知，按照龟兔赛跑的故事情节，兔子和乌龟的位移图象如图所示，下列关于兔子和乌龟的运动正确的
是（ ）A．兔子和乌龟是同时从同一地点出发的B．乌龟一直做匀加速运动，兔子先加速后匀速再加速C．骄傲的兔子在t₄时刻后奋力追赶，但由于速度比乌龟的速度小，还是让乌龟先到达预定位移S₃D．在0～t₅时间内，乌龟的平均速度比兔子的平均速度大

题型：未知 难度：其他题型

答案

A、由图可知兔子从t₁时刻开始运动，而乌龟从t=0时刻即开始运动，故A错误．
B、由于s-t图象的斜率等于物体的速度，而乌龟的s-t图象的斜率保持不变，故乌龟做匀速直线运动．故B错误．
C、兔子在t₄时刻后奋力追赶，由于s-t图象的斜率等于物体的速度，故兔子的速度大于乌龟的速度，但由于运动的时间过短，故在t5时刻当乌龟到达终点时兔子还没有到达终点，故C错误．
D、在0～t₅时间内，由于乌龟的位移大于兔子的位移，故乌龟的平均速度比兔子的平均速度大．故D正确．
故选D．

点击查看匀变速直线运动知识点讲解,巩固学习

解析

该题暂无解析

考点

据考高分专家说，试题“龟兔赛跑的故事源于伊索寓言，可谓众所周知.....”主要考查你对 [匀变速直线运动 ]考点的理解。

匀变速直线运动

定义：
在任意相等的时间内速度的变化相等的直线运动，即加速度恒定的变速直线运动叫匀变速直线运动。

特点：
a=恒量。

匀变速直线运动规律(基本公式)：
速度公式：v=
位移公式：x=
速度平方公式：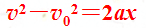
位移—平均速度关系式：x=

匀变速直线运动的几个重要推论：

1. 在任意两个连续相等的时间间隔内通过的位移之差为一恒量，即：S_Ⅱ－S_Ⅰ＝S_Ⅲ－S_Ⅱ＝…＝S_N－S_N－1＝ΔS＝(此公式可以用来判断物体是否做匀变速直线运动)。进一步推论：S_n＋m－S_n＝，其中S_n、S_n＋m分别表示第n段和第(n＋m)段相等时间内的位移，T为相等时间间隔。
2. 某段时间内的平均速度，等于该段时间的中间时刻的瞬时速度，即。
3. 某段位移中点的瞬时速度等于初速度v₀和末速度v平方和一半的平方根，即v_s/2＝。

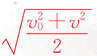null

null

null